Численная реализация упругопластической модели грунта
Идеализация модели грунтового основания осуществляется следующим образом. Если при внешнем или внутренним воздействии усилий напряжение грунта характерного объема меньше предельного
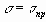
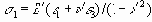
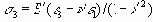
Здесь
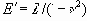
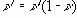
Предельные напряжения в области растяжения ограничиваются прочностью на растяжение

Таким образом, область I в зоне растяжения ограничивается напряжением
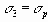
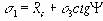
(5.2)
где Rc – прочность на одноосное сжатие
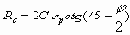

где C, j – удельное сцепление и угол внутреннего трения.
Последовательность упругопластического решения следующая. Нагрузка прикладывается малыми ступенями в той последовательности, в какой происходит реальное воздействие. Напряжения




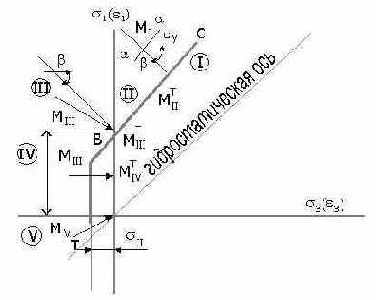
Рис. 5.1 Схема модели грунта
Матрица жесткости системы (МЖС) формируется один раз и в процессе решения остается постоянной. Для каждой ступени нагружения решается система уравнений с вектором сил


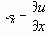

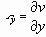
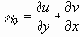

рассчитываются относительные деформации
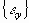
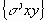
Найденные “упругие” напряжения суммируются с ранее накопленными
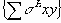
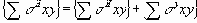
вычисляются главные суммарные напряжения
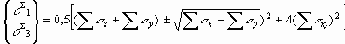
и угол a между s1 и осью х
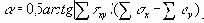
Производится сравнение
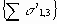
Если определяемая точка с координатами
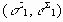
Если точка оказывается вне контура текучести, то находятся “теоретические” напряжения в следующем порядке. Если точка суммарных напряжений Мп попадает в область II (основная область пластичности), то “теоретическая” точка Мпт лежит на пересечении границы текучести с прямой Мп и Мпт. Угол наклона b прямой
Мп Мпт определяется законом течения и задан. При равнообъемном течении поверхность пластического потенциала параллельна гидростатической оси, при этом
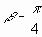
При известных координатах точки МII
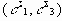
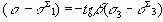
Уравнение предельной линии BC описано формулой (5.2). Совместное решение уравнений (5.7) и (5.2) относительно s1 и s3 дает координаты точки Мпт – теоретические напряжения:
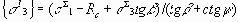
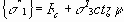
При
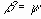
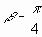
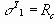
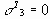
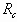
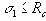
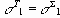
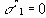
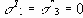
Если параметры границ текучести с,


Разница между исходными суммарными и теоретическими напряжениями рассматривается как “начальные” главные напряжения
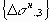
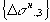
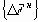
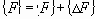
Начальные напряжения цикл за циклом в пределах шага накапливаются:
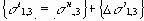
Если необходимая точность достигнута, то прикладывается следующая ступень нагрузки, если нет, то вырабатывается признак продолжения итераций и программа возвращается вновь на вычисление узловых перемещений, но уже при новых значениях
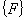
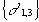
При реализации вышеприведенного алгоритма УП решения в программе “Геомеханика CREEP” рассмотрена изотропная среда с равнообъемным течением.
